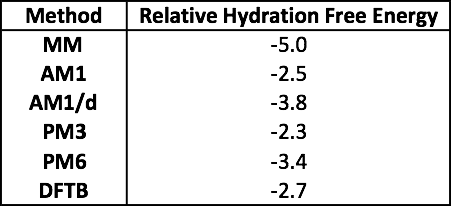
The table above shows the relative hydration free energy between PHE and TRP for all of the models (in kcal mol-1). These compare to the experimental value of -5.1 kcal mol-1.

Question 7.1 - The experimental relative hydration free energy is very close to that calculated using MM (the experimental value is only 0.1 kcal mol-1 more negative, which is well within the error margin of both experiment and the simulation). All of the QM/MM methods underestimate the experimental relative hydration free energy, although they all correctly predict that TRP is more soluble then PHE.

Question 7.2 - The best method is MM. This should come as no surprise as the MM parameters have been developed over many years to reproduce experimental properties such as hydration free energies. This doesn’t mean that the MM calculation is “right”. Rather, the MM calculation has been developed so that is gives the correct free energy. Examination of the structure of water in the solvation shells around each side-chain will show that water adopts conformations that do not match up with experiment (e.g. we are using a TIP3P water model that fails to show a second solvation shell). The QM/MM models are more physically accurate, but don’t benefit from the fortuitous cancellation of errors that benefit MM calculations (the MM models of the side-chains and water are all “equally poor”, so the errors in the model are roughly equal and cancel out). While the QM model of the side-chain is more physically accurate, the boundary between the QM side-chain and MM water is not modelled well. The fixed charges of the MM water molecules are unable to reflect back the polarisation of the QM side-chain, leading to over-polarisation. Methods of improving the interface could include scaling down the charges of the water molecules in the QM/MM calculation, or switching to a polarisable water model.

The take-home lesson from this workshop is that making one part of a model physically more accurate does not necessarily improve the result. Building multiscale models is inherently difficult and must be performed with care. The interface between the two levels can lead to non-physical effects and this must be checked for and corrected. In addition, improving one part of the model may lead to you losing the fortuitous cancellation of errors that can occur when all parts of the model are “equally poor”. However, once you have built a good multiscale model, you can use the techniques presented in this workshop to calculate “correction free energies” to calculate higher-quality multiscale free energies. As you have seen, this process is automated for QM/MM models in quantomm, which is a free to use and efficient tool for these kind of calculations.

← Back