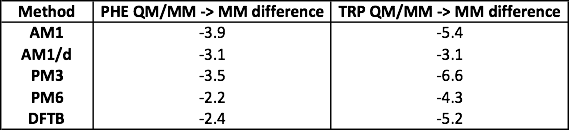
An example table is above. Note that the exact values you calculate will be slightly different, as these are averages calculated from a Monte Carlo simulation. Note also that the less negative the average energy difference, the closer the QM/MM interaction energy is to the MM energy, and thus the stronger the QM/MM interaction energy (as the MM interaction energy is the most negative, and hence the strongest).

Question 2.1 - The average difference in interaction energy is (generally) smaller in magnitude compared to the single-point energies calculated in exercise 1. This is likely because the structure used for the single-point energy was taken from the MM molecular dynamics simulation, so was a high probability structure for the MM model. In contrast, the average energy difference was calculated over an ensemble of structures sampled from the QM/MM ensemble, and so contained structures that were high-probability (and thus optimised) for the the QM/MM model.

Question 2.2 - From the average energy differences calculated above, AM1/d again gives the strongest interaction energy for TRP, while PM6 gives the strongest interaction energy for PHE (closely followed by DFTB, which had the strongest single-point interaction energy in exercise 1). While averaging has reduced the energy difference compared to MM, the QM/MM interaction energies between the side-chains and water are still weaker than the MM interaction energies.

Question 2.3 - No you wouldn’t expect every run of sample.py to give you the same result. This is because sample.py is performing a Monte Carlo simulation with a different set of random numbers used for every run. You could estimate the error on the average either by looking at the standard deviation and calculating a standard error, or by running multiple Monte Carlo simulations and looking at the spread of results.

← Back